The Socceroos win last night was very exciting, largely due to the penalty shootout. Penalty shootouts are exiting because they are zero-sum games (one player wins, the other loses). Although zero-sum games are relatively rare in real life they are a common feature of popular 'artificial' games such as chess, rock-paper-scissors, etc.Game theory suggests that when playing a zero-sum game you should keep your opponent guessing. For example, in rock-paper-scissors you should choose each strategy with a probability of a third, ensuring that your expected payoff is equal regardless of which 'tool' you use. Note that if they weren't equal, and you chose rock more often (since as Bart would say "nothing beats rock"), then your opponent could chose paper all the time and win more than 50 per cent of the games.
Penalty shoot-outs are very similar. For simplicity let's assume that a kicker has two options (shoot left or shoot right) and the keeper also has two options (jump left or jump right, where left and right are defined from the kicker's perspective). Like rock-paper-scissors, it will be best if the kicker keeps the keeper guessing and alternates between kicking to the left or the right. But, unlike rock-paper-scissors, the kicker will probably be better at kicking one way or another. Thus, to keep his payoffs equal he will kick more to his strong side than to his weak side (but he wouldn't make all his kicks to the strong side since the keeper can counter that by always jumping that way). Likewise, the keeper will jump more to the kicker's strong side, than the kickers kick that way, because he can be confident that the kicker is more likely miss the goal completely when kicking to his weaker side (remember the keeper must also keep his expected payoffs equal).
All this is outlined more rigorously (and probably more accurately) in a paper by Chiappori, Levitt (of Freakonomics fame) and Groseclose. They show that a right foot kicker's strong side is the left, and vice-versa for a left foot kicker. They also apply the predictions of game theory to a few seasons of Italian and Spanish football.
But how does the theory match up against last night's game?
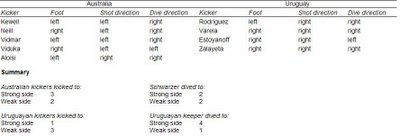The results show that the Australian players applied game theory more accurately (and eventually with more success) than their Uruguayan counterparts. Australian kickers did indeed choose their strong sides more than their weak sides (3-2), whereas the Uruaguayan kickers only kicked to their strong side once. Despite the praise being heaped on him today, Schwarzer went close to not applying game theoretic principles, but still chose the kicker's strong side twice more often than the Uruguayan kickers did.As the stats show, ultimately game theory (and economics) were the winners. Australia can confidently thank its place in the World Cup due to its superior understanding (and application) of economic theory.
3 comments:
There is no necessary link between zero-sum games and mixed strategies, even though many zero sum games do have mixed strategies. The best example is a common value English auction (Common value: the thing has an objective value that everybody knows. English: increasing price, open outcry.). The only equilibrium has all bidders bidding their true value.
But an English auction is not a zero-sum game. Wikipedia defines a zero-sum game as "a situation in which a participant's gain (or loss) is exactly balanced by the losses (or gains) of the other participant(s)." This is not true in an English auction because the 'winner's' payoff is the difference between what he paid and what the objective value of the item is. This could negative, positive or zero. However, the losers payoff is always zero: they don't pay anything.
You're right in general, but there is a specific case where a common value auction can be zero sum. If the auction is viewed as a game between the bidders and the auctioneer, and both have a common value for the good, the game is zero sum since any gain to the winning bidder is a loss to the auctioneer. All other bidders have zero payoff anyway. Probably not the best example of my point though, particularly because the auctioneer has only one strategy.
Post a Comment